A volatilitás a hozam változékonysága. Ezt a változékonyságot a folytonos kamatozással számított hozam szórásával szokás mérni. A volatilitást leggyakrabban a napi záróárfolyamokból szokták számítani, de lehet heti, havi vagy óránkénti, sőt percenkénti adatokból is becsülni. Amennyiben a volatilitás konstans, akkor mindegy, hogy miből kiindulva számolunk, hiszen a [latex size="1"]\Delta T[/latex] időtartam alatti variancia [latex size="1"]\sigma ^{2}\Delta T[/latex], és ebből kell visszaszámolni a [latex size="1"]\sigma[/latex] értékét. A számításhoz szükséges képletek:

[latex size="1"]z_{t}=ln(\frac{S_{t}}{S_{t-1}})[/latex] [latex size="1"]V=\sigma ^{2}\Delta t=\sum_{k=1}^{n}\frac{(z_{t}-z)^{2}}{n-1}[/latex]

ahol n a megfigyelések száma.

[latex size="1"]\sigma =\frac{\sqrt{V}}{\sqrt{\Delta t}}[/latex]

Az időtáv mértékegysége az év. Ha heti adatokkal dolgozunk, akkor [latex size="1"]\Delta t= \frac{1}{52}[/latex]. Ha [latex size="1"]\sigma _{heti}[/latex] jelöli a heti adatokból becsült heti volatilitást, akkor a heti és az éves volatilitás kapcsolata:

[latex size="1"]\sigma =\frac{\sigma _{heti}}{\sqrt{\frac{1}{52}}}=\sigma _{heti}\sqrt{52}[/latex]

Ha napi adatokból számítjuk a volatilitást, akkor az átszámítási képlet

[latex size="1"]\sigma =\sigma _{napi}\sqrt{252}[/latex]

mivel egy évben hozzávetőleg 252 munkanap van, és statisztikai elemzések azt mutatták, hogy az árfolyamok változása inkább kötődik a tőzsdei, mint a naptári napok számához (a hétvégén nem háromszor akkora az árfolyamváltozás, mint hét közben). Megjegyezzük, hogy a megfigyelések n száma nem azonos azzal, hogy hány részre bontottuk a vizsgálni kívánt időszakot.

Minél nagyobb egy részvény volatilitása, annál nagyobb kilengések jellemzik az árfolyam alakulását. A statisztikai volatilitás az áringadozás statisztikai módszerekkel megállapított százalékos értéke. A statisztikai volatilitás értékének meghatározásához a kereskedők és elemzők általában egy adott időszak piaci elszámoló árainak normális eloszlását vizsgálják. Persze, ha feltételezzük, hogy az ár értéke sohasem lehet nulla vagy negatív, akkor a lognormális eloszlást érdemes használni, ami viszont egy kis adatfeldolgozást igényel. A 22.6 %-os volatilitás egyszerűen az árhányadosok lognormális sorának a 252 tőzsdenapra vetített normális szórása, így kaphatunk éves statisztikát. Összesen 20 nap elszámoló áraiból képezhetjük a sorozatot, mert úgy érezhetjük, ezen időszak híven tükrözi a piaci áringadozásokat. A sorozat elkészítéséhez kevesebb vagy több adat is felhasználható, de legalább 15-20 napos időszakot vegyünk alapul, hogy statisztikailag elfogadható eredményt kapjunk. Ha valahol azt halljuk, hogy az alaptermék volatilitása 10 %, akkor az alaptermék ára az esztendő során

• -10% és +10% határok között fog mozogni, meglehetősen magas, egészen pontosan 68%-os valószínűséggel,
• -2×10% és +2×10% határok között 95.4%-os valószínűséggel,
• -3×10% és +3×10% határok között 99.7%-os valószínűséggel.

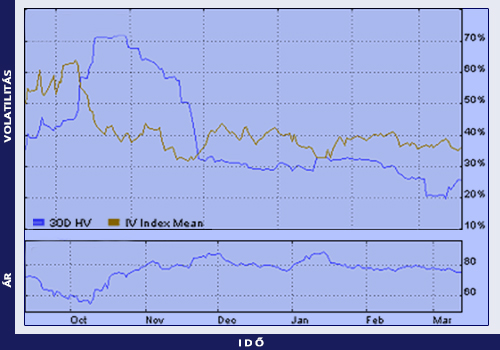
Az alábbi táblázatban különböző periódusok esetén számolt statisztikus volatilitás értékek láthatók. Tapasztaljuk, hogy a 10 napos 19.34%-os érték relatíve kicsiny, míg a 120 napos 43.03%-os érték relatíve magas. A volatilitást ábrázoló chart-on pedig azt látjuk, hogy a 30 napos volatilitás az októberi 72%-ról 19.83%-ra csökkent márciusban. A csökkenő volatilitást az októberben kezdődő emelkedő részvényár kíséri.

Historikus volatilitás, IV index és árfolyam az IBM részvényére

Összefoglalva, a történeti volatilitás az alaptermék relatív mozgását méri. Egy matematikai kifejezés, amely %-ban adja meg, hogy a termék ára milyen mértékben mozgott fel vagy lefelé az elmúlt időszakban. A termék statisztikai volatilitása folyamatosan változik, értékét naponta kell újra számolni, a kapott érték jelentős változásokat tud produkálni egyik napról a másikra, ezért szokásos egy 10 vagy 20 napos mozgó átlagot kalkulálni a későbbi munkához. Ezt a mozgó átlagot tudjuk a későbbiekben felhasználni a fair érték kiszámítására a különböző opciós modellekben. A mindennapi gyakorlatban használhatjuk annak eldöntésére, hogy egy adott ármozgás bekövetkezésének vagy meg nem történésének mekkora a valószínűsége, és ha ismert a határidős kontraktus statisztikai volatilitása és a jelenlegi piaci ára, akkor kiszámítható, hogy egy adott árat adott időintervallumon belül mekkora valószínűséggel fog elérni vagy, hogy eléri-e egyáltalán.