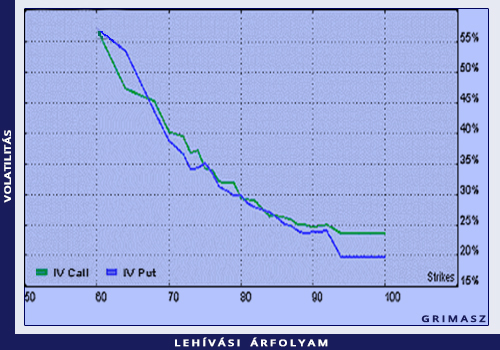
Joggal gondolhatnánk, hogy egy adott alapterméknek egy meghatározott időszakra vonatkozóan adott nagyságú volatilitása van, és a különböző lehívási árfolyamú opciók visszaszámított volatilitása ezzel azonos. Az még magyarázható, ha a különböző futamidejű opciók visszaszámított volatilitása különbözik. Az azonban már végképp furcsa, hogy adott futamidejű, de más-más lehívási árfolyamú opcióknak eltérő a visszaszámított volatilitása. Már pedig ez a helyzet. Ezt nevezik a volatilitás mosolyának (volatility smile). A volatilitás mosolyához hasonlóan beszélünk a volatilitás lejárati szerkezetéről is (term structure of volatility).
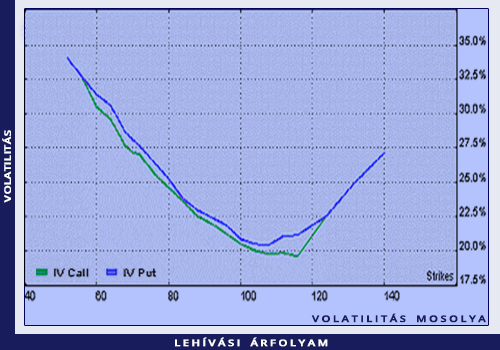
A volatilitás mosolya az ugyanarra az alaptermékre vonatkozó, azonos futamidejű, eltérő lehívási árfolyamú opciók visszaszámított volatilitásainak az ábrája a lehívási árfolyam függvényében.
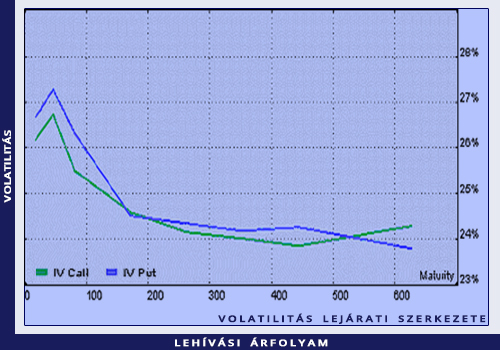
A volatilitás mosolya – Volatility smile
A volatilitás lejárati szerkezete az az ábra, amely ugyanarra az alaptermékre vonatkozó, azonos lehívási árfolyamú, eltérő futamidejű opciók visszaszámított volatilitásait írja le a futamidő függvényében.
A volatilitás lejárati szerkezete ATM opciók esetében a DJX indexen
A Black-Scholes-modellben mindkét ábra vízszintes egyenes. A valóságban a visszaszámított volatilitás annál a lehívási árfolyamnál szokott a legkisebb lenni, amelyik megegyezik a forward árfolyammal, míg az ennél nagyobb, illetve kisebb lehívási árfolyamok mellett a visszaszámított volatilitás nagyobb. Ha ez a helyzet, akkor egy derűs mosollyal van dolgunk.
Az utóbbi időben nem ritka azonban, hogy valamelyik szájsarok legörbül, innen a grimasz elnevezés, angolul volatility smirk.
Volatilitás grimasz a DJX indexre (lejárat 2003 áprilisában)
A volatilitás mátrixa az a táblázat, amely az ugyanarra az alaptermékre vonatkozó opciók visszaszámított volatilitásait a futamidő és a lehívási árfolyam függvényében rendezi össze.
