Options are contracts granting the right to the option holder (buyer) to sell or buy an underlying security at an agreed-upon price (strike price) on a specific future date. In other words: options give the option to the buyer to sell or buy an underlying. In the same time, options generate an obligation to the seller of the option.
There are two types of options: call (buy) and put (sell). A call option offers the buyer the right, but not the obligation to buy. The seller (writer) of the option must perform on the contractual obligation to sell if the buyer decides to exercise his/her right to buy. On the contrary, a put option offers the buyer the right (but not the obligation) to sell. The seller of the option must perform on the contractual obligation to buy if the buyer decides to exercise his/her right to sell.
Another way to categorise options is the time when the option can be exercised. There are two main styles: European and American. European-style options can be exercised only at maturity, which is a specific future date. American-style options can be exercised any time between the time of purchase and maturity date.
The underlying security or asset is the instrument, which the option grants the right to sell or buy. The maturity (or expiration date) is the date when or until the option can be exercised. The strike price of the option is the agreed-upon price of the underlying. When buying a call option with a strike price of $50, at maturity the underlying can be bought for $50. The actual market price of the underlying at maturity does not matter.
Long Call Option
However, the right to buy is only exercised if the market price of the underlying at maturity is higher than $50. If the market price is below $50, it is not worth to exercise the option, because the underlying can be bought directly on the market for less.
Options can be categorised based on their market as well. There are exchange traded options and OTC (Over The Counter) options. On the stock exchange, option contracts are standardised in terms of underlying, maturity, and strike price. Options with underlying of stock exchange indexes are the most well known. Options for the S&P and Dow Jones indexes are very common and also liquid.
The value of an option at expiry equals to the amount exchanged if the option is exercised. If the option does not worth to exercise, its value will be zero. Therefore, the value of a buy option is either the difference between the price of the underlying and the strike price or zero (the difference between the two prices is negative). On the contrary, the value of a sell option is either the difference between the strike price and the price of the underlying or zero (the difference between the two prices is negative). Before maturity, the value of the option depends on what type of option it is. Black-Scholes formula is used to determine European options’ value with an analytic approach.
However, analytic approach cannot be used for American options, valuation is only possible with numeric methods. The most well-know numeric method is the Binomial model.
Premium of an option
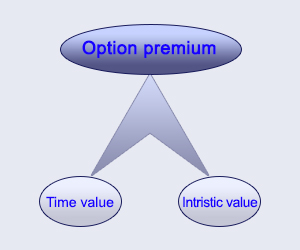
The value of an option can be divided into two factors: extrinsic (time) value and intrinsic value.
Intrinsic value is the amount an option would worth if it was exercised today (price of underlying - strike price). Time value makes up the remaining part: value of the option - time value. At maturity, the time value is zero and the value of the option equals to the intrinsic value.
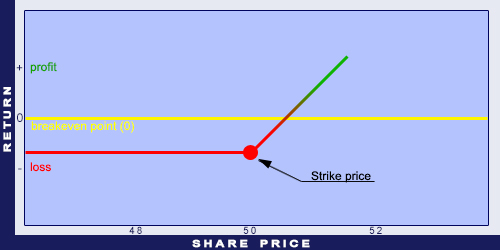
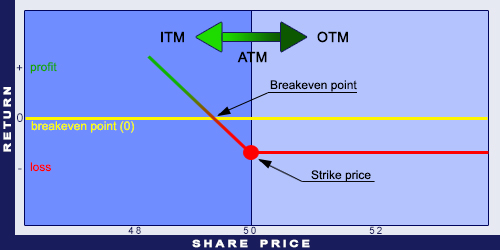
In the Money (ITM) options have intrinsic values. In case of a Call option it means that the price of the underlying is higher than the strike price. For Put options it is the opposite: the price of the underlying is lower than the strike price. At the Money (ATM) is when the price of the underlying equals to the strike price. Out of the Money (OTM) options have no intrinsic values: for Call options the strike price is higher than the price of the underlying and for Put options it is the opposite: the strike price is lower than the price of the underlying. The diagram below illustrates the definition of the ITM, the ATM, and the OTM cases.
ITM, ATM, and OTM for Call options
For Put options, ITM, ATM, and OTM can be visualised the following way:
ITM, ATM, and OTM for Put options
Implied Volatility is an important factor for pricing options. The Black-Scholes option pricing model relies on this value as well. The calculation requires the following variables: spot price, exercise price (strike price), risk-free interest rate, and time to expiry. Most NASDAQ shares (especially the technological securities) have larger volatility than financial instruments traded on other exchanges, such as the NYSE. This is directly observable from the price of the options.
