Leírás és módszer

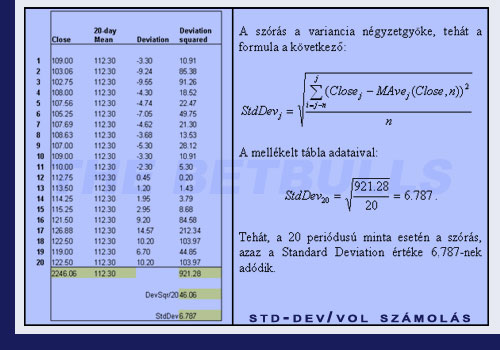
A Standard Deviation, vagyis a szórás egy statisztikai mérőszám, mely jelzéseket szolgáltat a volatilitással kapcsolatosan. A szórás a minta elemeinek szóródását jellemző mérőszám, mely megegyezik a variancia négyzetgyökével. Méri az átlagtól való eltérést (záró árak). Minél nagyobb a különbség a záró érték és az átlagos záró érték között, annál nagyobb lesz a szórás és a volatilitás értéke. Következésképp, minél kisebb a különbség a záró érték és az átlagos záró érték között, annál kisebb a szórás és a volatilitás. A minta elemeinek eloszlását jellemző szórás nemcsak különböző minták összehasonlítására használható, hanem egy adott minta elemzésekor is lényeges információt mutat. A minta számtani középértékéhez hozzáadva vagy kivonva egyszeres vagy többszörös szórásnyi terjedelmeket, normális eloszlás esetén olyan értéktartományokat kapunk, amelyekbe a minta jól meghatározott részei tartoznak. Kiszámítása n elemű minta esetén a következőképpen történik:

• Amennyiben nem tettük meg, számoljuk ki a variancia értékét. A varianciát úgy számoljuk ki, hogy minden egyes elemnek az átlagtól való eltérését négyzetre emeljük, ezeket az értékeket összeadjuk, majd elosztjuk az n elemszámmal.
• Végül vonjunk négyzetgyököt az előző lépésben kiszámolt varianciából.

Standard Deviation / Volatility számítása példával illusztrálva

Mivel a Standard Deviation-t a felső és alsó Bollinger Szalagok közötti szórást határozza meg, a Bollinger Band Width indikátor helyettesítheti a Standard Deviation indikátort. A Standard Deviation értékének kétszeres adja a Bollinger Band értékét, tehát a Bollinger Band Width indikátort el kell osztani kettővel, hogy megkapjuk az aktuális Standard Deviation-t.

Példák

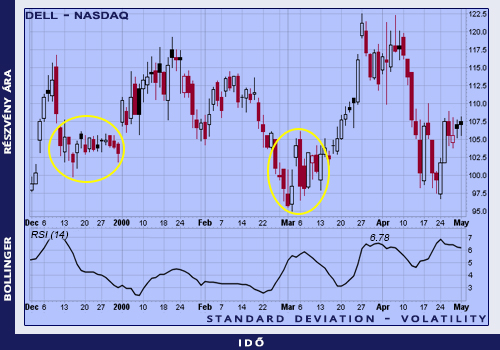
Az alábbi példában megfigyelhetjük, hogy egy kiterjedt konszolidációs periódus után a Standard Deviation csökkent. Figyeljük meg a késői decemberi időszakot, ahol is a kereskedés szűk ársávban mozgott. Ekkor a volatilitás újból lecsökkent. Március közepe fele a részvény ismét szűk csatornába mozgott, ahol a volatilitás megint csak alacsony értékű volt. Azonban március második felében a volatilitás nagymértékben megemelkedett. Az opciós piacra érvényes a következő állítás: minél magasabb a volatilitása az adott részvénynek, annál többet ér az opció prémiuma, illetve minél kisebb a volatilitása az adott részvénynek, annál alacsonyabb az opció prémiuma.

Példa az alacsony és magas volatilitásra

 Volatilitás

A volatilitás az árfolyamváltozás alsó és felső lehetséges határát (szórását) méri meghatározott valószínűségi szint mellett éves százalékos formában. Megadja a stop-loss szinteket, ugyanis segítségével meghatározható az a felső és alsó szintje az árfolyamnak melyet egy meghatározott valószínűség mellett az árfolyamgörbe lefelé és felfelé nem lép át. Továbbá, figyelmeztet a potenciális trendváltozásra. Ha a piac trendszerűen viselkedik és a volatilitás ezzel egyidejűleg magas, akkor ebben a szituációban a volatilitás erőteljes csökkenése a trend végének közeledtét, az árfolyamok torlódását jelzi. Ha az árfolyamok torlódnak, vagyis trend nélkül oldalmozgást végeznek alacsony volatilitás mellett, akkor egy hirtelen emelkedés a volatilitásban a piac trend irányába történő elmozdulását vetíti előre. A trendfordulót az árfolyamváltozásnak is meg kell erősítenie, például azzal, hogy a záró árfolyam áttör egy fontos támasz vagy ellenállási szintet. Számítása a következőképpen történik:

$Volat(j)=\sqrt{k\times SMA_{j}\left (( X(j)-SMA_{j}(X,N) \right )^{2},N-1)}$

ahol

$X_{i}=ln\frac{ZaroAr(i)}{ZaroAr(i-1)}$

Számolnunk kell még az idő-normalizáló együtthatót is.